Information Center
Since the beginning of the study of surfactant solutions, it was recognized that the physical properties of these solutions, such as surface tension, electrical conductivity and detergency, show an abrupt change in the neighborhood of a critical micelle concentration. These unusual properties indicated the formation of molecular aggregates. The formation of colloidal-sized clusters of individual surfactant molecules in solution is now better known as micellization. Although first suggested by McBain in 1913, the earliest concrete model for spherical micelles is attributed to Hartley (1). Figure 1 shows schematically the three environments in which surfactant molecules reside in a typical (aqueous) surfactant solution. Surfactant molecules disperse as monomers in the aqueous phase, form aggregates (micelles), or adsorb as a film at the air/water interface. The surfactant is in dynamic equilibrium between these states. Thus, at a given temperature, pressure and concentration, the number of monomers, micelles and monomers adsorbed at the air/water interface is fixed under equilibrium conditions.
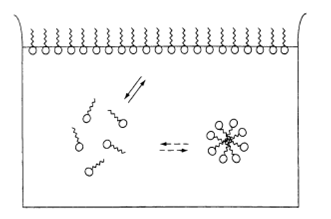
Figure 1. Schematic representation of the three states in which surfactant molecules reside in water, i.e. monomers adsorbed at the air/water interface, monomers in the bulk solution and micelles
The process of surfactant clustering or micellization is primarily an entropy-driven process. When surfactants are dissolved in water, the hydrophobic group disrupts the structure of water and therefore increases the free energy of the system. Surfactant molecules therefore concentrate at interfaces, so that their hydrophobic groups are directed away from the water and the free energy of the solution is minimized. The distortion of the water structure can also be decreased (and the free energy of the solution reduced) by the aggregation of surface-active molecules into clusters (micelles) with their hydrophobic groups directed toward the interior of the cluster and their hydrophilic groups directed toward the water. However, the surfactant molecules transferred from the solution to the micelle may experience some loss of freedom from being confined to the micelle. In addition, they may experience an electrostatic repulsion from other similarly charged surfactant molecules in the case of ionic surfactants. These forces increase the free energy of the system and oppose micellization. Hence, micelle formation depends on the force balance between the factors favouring micellization (van der Waals and hydrophobic forces) and those opposing it (kinetic energy of the molecules and electrostatic repulsion). The explanation for the entropy-dominated association of surfactant molecules is called the "hydrophobic effect" or "hydrophobic bonding" (2).
The concentration of surfactant at which micelles first appear in solution is called the critical micelle concentration or CMC. Representing the surfactant by S, the micellization process can be described by the following reaction:
 (1)
(1)
in which Sn is the micelle with a degree of aggregation n. The formation of micelles from the constituent monomers involves a rapid, dynamic, association-dissociation equilibrium. Micelles are undetectable in dilute solutions of monomers, but become detectable over a narrow range of concentrations as the total concentration of surfactant is increased, above which nearly all additional surfactant species form micelles. The concentration of free surfactant, counterions and micelles as a function of the overall surfactant concentration is shown in Figure 2. Above the CMC, the concentration of free surfactant is essentially constant, while the counterion concentration increases and the micellar concentration increases approximately linearly.
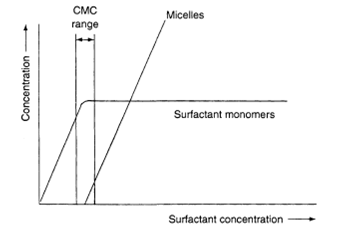
Figure 2. Concentration of individual species in a surfactant solution
The concentration at which micelles first become detectable depends on the sensitivity of the experiment used to determine the CMC. The purpose of this chapter is to discuss the experimental methods that have been used to determine the critical micelle concentration for aqueous systems, as well as to give an overview of CMC determination techniques for surfactants in non-aqueous media.
1, IMPORTANCE OF critical micelle concentration (CMC)
The value of the critical micelle concentration (CMC) is an important parameter in a wide variety of industrial applications involving adsorption of surfactant molecules at interfaces, such as foams, froths, emulsions, suspensions, and surface coatings. It is probably the simplest means of characterizing the colloid and surface behaviour of a surfactant solute, which in turn determines its industrial usefulness. Many industrial processes are also dynamic processes in that they involve a rapid increase in interfacial area, such as foaming, wetting, emulsification and solubilization. First, the available monomers adsorb on to the freshly created interface. Then, additional monomers must be provided by the breakup of micelles. Especially when the free monomer concentration (i.e. CMC) is low, the micellar breakup time or diffusion of monomers to the newly created interface can be rate-limiting steps in the supply of monomers, which is the case for many nonionic surfactant solutions (3).
Experimentally, the CMC is determined from the discontinuity or inflection point in the plot of a physical property of the solution as a function of surfactant concentration. This is demonstrated in Figure 3 (4). Clear breaks of almost every measurable physical property that depends on size and number of particles in solution are shown by all types of surfactants, i.e. nonionic, anionic, cationic and zwitterionic, in aqueous media. A wide variety of techniques involving the measurement of physical properties have been used to determine CMC values. The experimental methods by which the CMC of surface-active agents in aqueous solution may be determined are discussed in the next section.
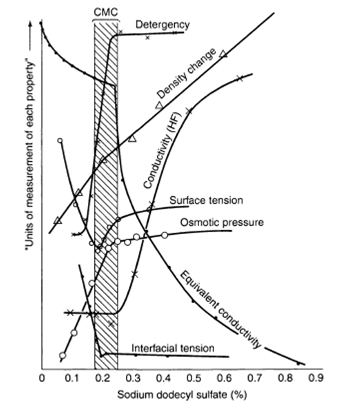
Figure 3. Changes in some physical properties for an aqueous solution of sodium dodecyl sulfate (SDS) in the neighborhood of the CMC (from ref. (4)), reprinted with permission from American Chemical Society
2, METHODS TO DETERMINE critical micelle concentration (CMC) by surface tension method
A large number of methods have been applied to the determination of the critical micelle concentration of surface-active agents. Most of the physico-chemical property changes can be used to determine the CMC, provided that the measurement can be carried out accurately. For an extensive compilation of the CMCs of surfactants in aqueous and non-aqueous media, the reader is referred to books by Mukerjee and Mysels (5), Rosen (6), and more recently by van Os et al. (7), and references therein.
The surface tension of aqueous solutions of surface active agents decreases very rapidly until the CMC is reached and then stays constant above the CMC. Above this concentration, the surface tension of the solution remains constant since only the monomeric form contributes to the reduction of the surface or interfacial tension. For concentrations below, but near the CMC, the slope of the curve is essentially constant, indicating that the surface concentration has reached a constant maximum value. In this range the interface is considered to be saturated with surfactant molecules and the continued reduction in the surface tension is mainly due to the increased activity of the surfactant in the bulk, rather than at the interface.
The equilibrium surface tension can be measured by a variety of methods, such as the Wilhelmy plate, du Nouy ring, drop weight or by volume and shape of the drop (see Chapter 11 earlier). The data are generally plotted against the logarithm of concentration as the abscissa and the transition between a descending line (often assumed to be straight) and another one close to the horizontal is taken as the CMC. In the case where the concentration of surfactant is plotted linear against the surface tension, the curvature of the descending portion is much less sharp. If the sample contains highly surface-active impurities, however, the inflections in the surface tension versus log concentration plot become more ambiguous and show a minimum (see the surface tension curve in Figure 3). The presence of a minimum is often observed for technical-grade nonionic surfactants, due to the broad molecular weight distribution owing to the degree of ethoxylation, and ionic surfactants that are partially hydrolysed (e.g. long-chain alcohols). This minimum disappears as the impurity dissolves in the micelles above the CMC. The surface tension method is very sensitive to impurities, since it only measures the surface concentration of all surface-active species present in solution and does not detect the presence of micelles in the bulk. Therefore, it is recommended that other techniques being applied as well to confirm the CMC values obtained by the surface tension method.
From the surface tension versus log concentration curves thus obtained, a very useful parameter can be derived, namely the area per molecule of the surfactant. As early as 1878, Gibbs derived a differential equation relating the surface tension, the number of moles and the chemical potentials of the components at the interface, as follows:
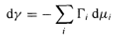 (2)
(2)
where dγ is the change in interfacial tension of the solvent, Гi - is the surface excess concentration, which can be approximated by the number of moles per unit area, and dui, is the change in chemical potential of the components in the system. The Gibbs equation can be used to calculate the surfactant concentration at the interface, and hence the area per molecule from the simple measurement of surface tension. For dilute solutions of a nonionic surfactant or a 1:1 ionic surfactant in the presence of electrolyte, equation (2) can be written as follows:
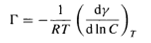 (3)
(3)
where R is the gas constant, T the absolute temperature and С the concentration of surfactant (8). The surface excess concentration, Г, can be obtained from the slope of a plot of the surface tension у versus In С at constant temperature, which then can be used to calculate the area per molecule a (in squared angstroms) from the following relationship:
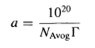 (4)
(4)
where NAwog is the Avogadro constant and Г is the surface excess concentration. An extensive list of areas per molecule for a variety of surfactants and counterions is given by Rosen (6).
3, METHODICAL DIFFERENCES IN DETERMINING critical micelle concentration (CMC)
As common methods used for the determination of the CMC, a series of measurements of some property of the surfactant solution as a function of surfactant concentration is usually involved. This is followed by the detection of some characteristic point - which is called the CMC. Methodical differences may originate from the choice of the characteristic point, the kind of plot on which this point is chosen, the kind of data which are plotted and the effect of the dye. The CMC is not a very sharply defined point above which properties are qualitatively different from those below. In fact, all properties of a solution in the CMC region vary in a continuous manner and so do all of their derivatives. A micelle is by definition a reversible aggregate of a large but not infinite number of monomers. The micelle formation reaction must obey the laws of chemical equilibrium and, as such, the concentration
dependence of the degree of micellization has to change gradually. Consequently, all properties of the solution must show similarly rapid but gradual changes. In addition, it is well understood that there is not a unique number of monomers which can form a micelle but a range with relatively wide limits. Hence, micelles are polydisperse (15). This is in agreement with the fact that the average micellar size continuously varies with conditions, such as temperature, counterionconcentration or other additives, nature of the counterion, chain length and structure. In conclusion, the CMC region contains many micelles of different aggregation number, each with a different concentration dependence, which further spreads and complicates the changes of bulk properties occurring in this region.
4, REFERENCES
1. Hartley, G. S., Aqueous Solutions of Paraffin Chain Salts, Hermann, Paris, 1936.
2. Tanford, C, The Hydrophobic Effect. The Formation of Micelles and Biological Membranes, 2nd Edn, Wiley, New York, 1980.
3. Patist, A., Oh, S. G., Leung, R. and Shah, D. O., Kinetics of micellization: its significance to technological processes, Colloid Surf., A, 176, 3-16 (2001).
4. Preston, W. C, Some correlating principles of detergent action, J. Phys. Colloid Chem., 52, 84-96 (1948).
5. Mukerjee, P. and Mysels, K. J., Critical Micelle Concentrations of Aqueous Surfactant Systems, NSRDS-NBS 36, US Department of Commerce, Washington, DC, 1971.
6. Rosen, M. J., Surfactants and Interfacial Phenomena, 2nd Edn, Wiley, New York, 1989.
7. van Os, N. M., Haak, J. R. and Rupert, L. A. M., Physico-Chemical Properties of Selected Anionic, Cationic and Nonionic Surfactants, Elsevier, Amsterdam, 1993.
8. Hiemenz, P. C. and Rajagopalan, R., Principles of Colloid and Surface Chemistry, 3rd Edn, Marcel Dekker, New York, 1997, pp. 297-354.
9. Debije, P., Light scattering in soap solutions, Ann. N.Y. Acad ScL, 51, 575-592 (1949).
10. Anacker, E. W., Micelle formation of cationic surfactants in aqueous media, in Cationic Surfactants, Jungermann, E. (Ed.), Marcel Dekker, New York, 1970, pp. 203-309.
11. Berne, B. J. and Pecora, R. (Eds), Dynamic Light Scattering, Wiley, New York, 1976.
12. Patist, A., Bhagwat, S. S., Penfield, K. W., Aikens, P. and Shah, D. O., On the measurement of critical micelle concentrations of pure and technical-grade nonionic surfactants, J. Surf. Det., 3, 53-58 (2000).
13. Stilbs, P., Fourier transform pulsed-gradient spin echo studies of molecular diffusion, Progr. NMR Spectrosc, 19, 1-45 (1987).
14. Weissler, A., Fitzgerald, J. W. and Resnick, I., A sound velocity method for determination of molecular weight of liquid polymers, J. Appl. Phys., 18, 434-438 (1947).
15. Lang, J. and Zana, R., Chemical relaxation methods, in Chemical Relaxation Methods in Surfactant Solutions - New Methods of Investigation, Zana, R. (Ed.), Marcel Dekker, New York, 1987, pp. 405-452.
16. Handbook Of Applied Surface And Colloid Chemistry - Vol 2 - K. Holmberg (ed) (Wiley, 2002)
Hot keywords of USA KINO:contact angle, contact angle measurement, contact angle meter, contact angle goniometer, surface tensiometer, interfacial tensiometer, surface tension measurement, surface tension, surface tensiometry, contact angle measurement equipment and device, calculating surfac free energy, Determining Critical Micelle Concentration (CMC) of surfactant, made in China Method for choosing surface tensiometer NEW Method for choosing contact angle meter (goniometer) NEW Method for choosing interfacial tension meter NEW

Manage technical support: www.chem17.com GoogleSitemap
MainPro : contact angle,contact angle meter,contact angle goniometer,surface tension,surface tensiometer